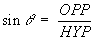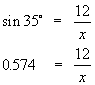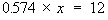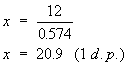Calculating the Hypotenuse

From: Carl Hastings
Date: 17 Feb 1999

Subject: Calculating the length of the hypotenuse with trigonometry

Our teacher set us this problem:

A triangle has corners A, B and T.
A and B are along the ground and T is above B.
The angle at B is 90° and the angle at A is 35°.
The length of BT is 12 metres.
What is the length of the diagonal AT ?

I used sin because side BT is opposite, but when I calculated 12×sin35°, I got the wrong answer. Where have I gone wrong?

Maths Help suggests:

The very first thing to do in a problem like this is to draw a diagram,
marking on the values you know. Call the unknown length "x".

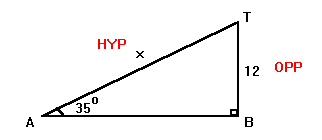
You know an angle, you know the opposite side and you want the hypotenuse.
So use the standard formula

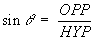
and replace the known quantities, giving:

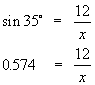
Now the unknown quantity is on the bottom of the fraction,
so multiply both sides by x:

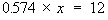
Finally, to obtain the value of x, divide both sides by 0.574

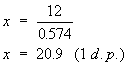
The length of AT is therefore 20.9 metres (to 1 d.p.)

You made the same mistake that many people make.
When the unknown quantity "x" is on the bottom of the fraction, you must do two steps:

First multiply both sides by x
Then divide both sides by the number which is multiplying the x to get x itself.

Return to topic list