
How do I solve the equation 2cos(x+50) = sin(x+40) for 0<=x<=360 degrees? |
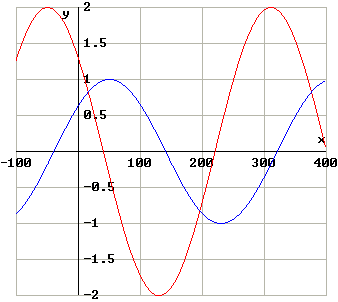
First, let us sketch the graphs of
y = 2cos(x+50) (in red)
and
y = sin(x+40) (in blue).
The solutions to your problem are the x-values of the points where the curves intersect.
There appear to be two solutions in the required range.
To solve the equation, use the trig. identities:
So: cos (x + 50) = cos x cos 50 - sin x sin 50
and sin (x + 40) = sin x cos 40 + cos x sin 40
You must solve
2(cos x cos 50 - sin x sin 50) = sin x cos 40 + cos x sin 40
Re-arranging,
cos x(2cos 50 - sin 40) = sin x(cos 40 + 2sin 50)
Dividing through by cos x and (cos 40 + 2sin 50)
![]()
This simplifies to:
tan x = 0.2796...
And the two solutions in the range 0 <= x <= 360 are:
x = 15.6°, 195.6° (1 d.p.)