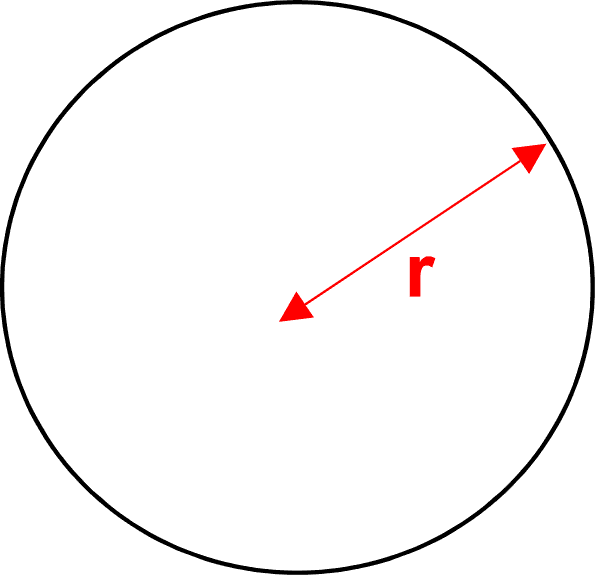
Start with the two well-known formulae:
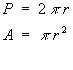
On our GNVQ engineering course we were set this problem: Show that the area of a circle is proportional to the square of its perimeter.Can you help me on this? To find the area or perimeter of a circle you need to know the radius, don't you? So how can you do this? |
Yes, the formula for the area and the perimeter (or circumference) of a circle are both functions of the radius. To get a relationship between the area and the perimeter, you need to eliminate the radius. Do it like this:
Start with the two well-known formulae:
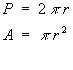
Make r the subject of the first:
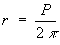
and substitute this into the second:
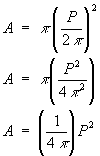
So, to 4 decimal places, we have the result
A = 0.0796 P2
which demonstrates that the Area is proportional to the Perimeter squared. The constant
of proportionality is 0.0796
Remember what is meant by "Y is proportional to X".
This means that you can show that Y = k.X
where k is a constant.
We have shown that Area (A) is proportional to the Perimeter squared (P2)
with the constant k being 0.0796 for circles.
It is a useful fact that the area of any regular two-dimensional shape is proportional to its perimeter. Let's run through a similar proof for squares.
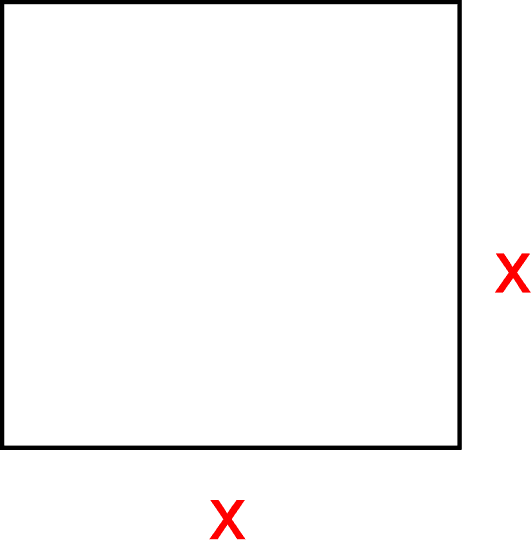Start with the two well-known formulae:
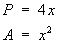
Make x the subject of the first:
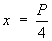
and substitute this into the second:
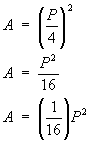
So, to 4 decimal places, we have the result
A = 0.0625 P2
which demonstrates that the Area is proportional to the Perimeter squared. The constant
of proportionality is 0.0625 for squares.