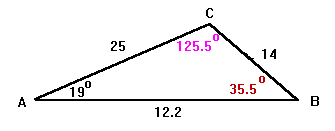
If your answer for angle B is 35.5° (in red) then angle C would have to be 125.5° (in pink).
But is this construction possible? Obviously not! For example, you have the shortest side opposite the largest angle . . . !

I used the sine rule for working out angle B in a triangle with
side a = 14 cm, angle A = 19°, side b = 25 cm
and side c = 12.2 cm. |
Well, let us show you first why your answer is wrong.
Using the data you gave, and the answer you found, the diagram of the
triangle would look something like:

If your answer for angle B is 35.5° (in red) then angle
C would have to be 125.5° (in pink).
But is this construction possible? Obviously not! For example, you have the
shortest side opposite the largest angle . . . !
Look back at your calculations.
When you applied the Sine Rule you probably had something like:
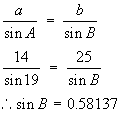
and from this you deduced that B = 35.5 degrees.
But don't forget that simple trig equations have two possible
solutions in the interval 0 to 360 degrees. In this particular question it
is the other solution that you need.

So the correct answer is that angle B = 144.5 degrees.
The fact that when you use the Sine Rule to find a missing angle there will be two possible answers is known as the ambiguous case. A diagram should be used (as we did above) to check which option is sensible.
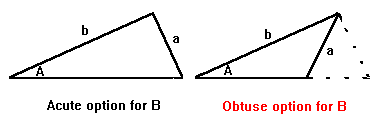
The ambiguous case can be illustrated in the sketch below, which shows that
there are two possible scenarios if you know angle A, side a and side b: