
After a holiday, Janet has ten coins in her purse: five 10 pence coins, three 1 franc coins and
two 1 mark coins. These coins are of similar size and colour. She takes out three coins at random.
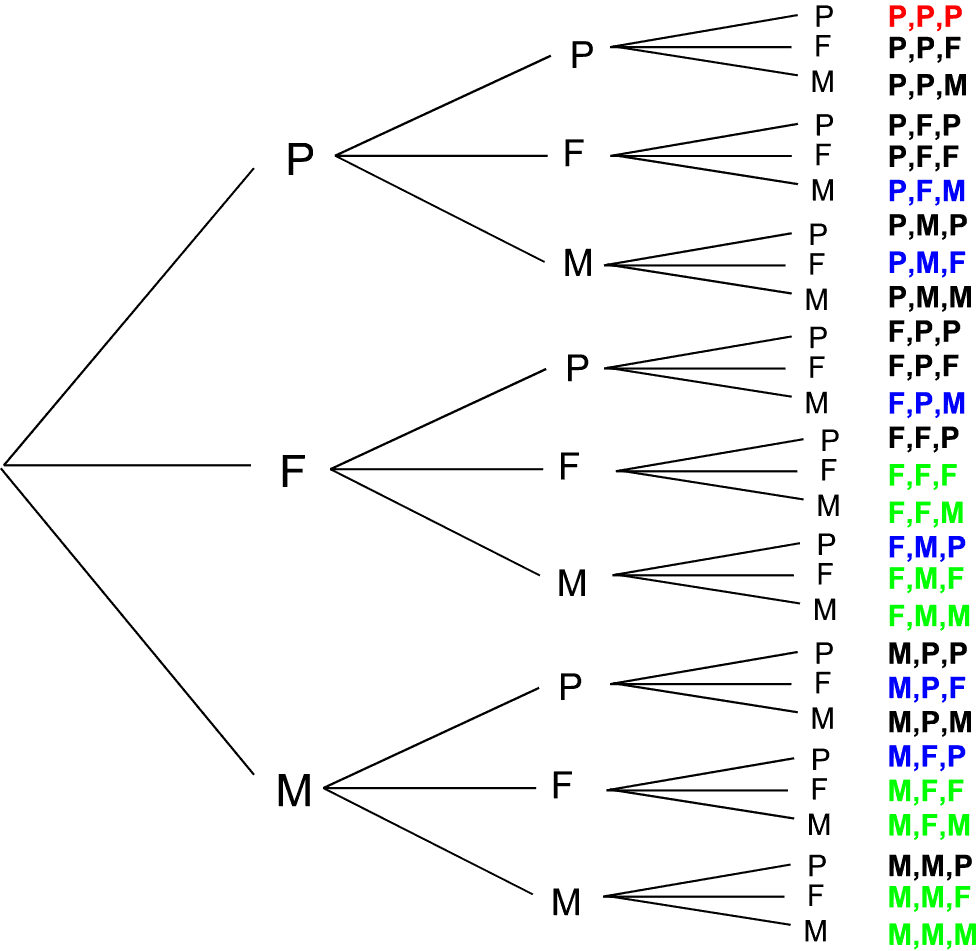
Draw a tree diagram to find the probability that |
This is quite a complicated tree diagram, for two reasons:
The overall structure of the tree diagram is shown below.
P means a 10 pence coins is taken
F means a 1 franc coin is taken
M means a 1 mark coin is taken

The probabilities of the first stage branches are out of 10:
Prob(P) = 5/10
Prob(F) = 3/10
Prob(M) = 2/10
The probabilities of the second stage branches are out of 9, since one coin was taken out on the
first stage, and the actual values of the probabilities will depend on which coin was
taken out first.
For example,
Prob(P if P first) = 4/9
but
Prob(P if F or M first) = 5/9
Similarly, the probabilities on the third stage branches will be out of 8. The actual values of the probabilities will depend on what the first and second coins were.
The answer to part (a), that all coins are 10 pence coins, is shown as the outcome P,P,P in
red at the end of the "pathway" along the branches of the tree which shows P first, P second and
P third.
The probability is found by multiplying the probabilities of the three P's together:
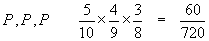
So the probability that all coins are 10 pence is 60/720 = 1/12
The answer to part (b), that none of the coins are 10 pence coins, is shown by the green
outcomes. Note that there are eight possible pathways which give the required result. The
probabilities of each of these is found by multiplying the individual probabilities of the
coins together along each pathway, and the answers added together:
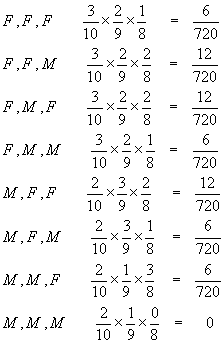
Adding these up gives the probability that none of the coins are 10 pence coins is 60/720 = 1/12
The answer to part (c), that all the coins are different types, is shown by the blue outcomes.
Note that there are 6 possible pathways:
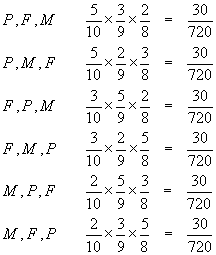
Adding these up gives the probability that the coins are different is 180/720 = 1/4