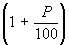
If the interest is applied monthly, then the monthly multiplier is
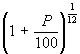
This means that if an amount A is outstanding at the beginning of the month, then the amount outstanding at the end of the month will be
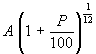

You borrow £5000 to finance a new car purchase, and repay it over
36 monthly instalments at an annual interest rate of 10% (APR). |
First a bit of background revision:
If the annual interest rate is P%, then the annual multiplier isIn this example, the annual APR is 10%. Therefore the monthly multiplier is
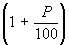
If the interest is applied monthly, then the monthly multiplier is
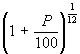
This means that if an amount A is outstanding at the beginning of the month, then the amount outstanding at the end of the month will be
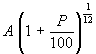

Our problem is to find the value of the monthly repayment. Call this r. We assume a
repayment is made at the end of each month.
We need to list the amount of the loan still outstanding at the end of each month, in order to
spot the underlying pattern.
We can see a pattern building up here. If you continue it yourself for a few more months you
should see that at the end of month 36 the amount outstanding can be written
5000q36 - rq35 - rq34 - rq33 - . . . . - rq2 - rq - r
This can be simplified by taking out a common factor of -r. Also, since we know that
the loan will have been paid off by the end of 36 months, this amount outstanding must be zero.
Therefore
5000q36 - r(q35 + q34 + q33 + . . . . + q2 + q + 1) = 0
Now our knowledge of Geometric Series comes in handy. In the brackets we have the sum of
36 terms of a Geometric Series with initial term 1 and common ratio q. Using the standard
formula for this, we end up with the following formula which has to be solved to find r:
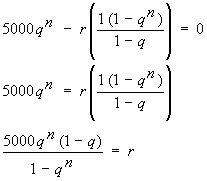
Replacing q by its known value (remember we used q = 1.00797414) gives
r = 160.33
Therefore the monthly repayment is £160.33.
NOTE 1: The above calculations were carried out on the assumption that a year consists of 12 equal months. In practice this is not the case, since some have more days than others. In the real world, banks often apply interest on a daily basis, which means the repayments quoted would be slightly different from the figure we found above.
NOTE 2: If we calculate the total amount repaid over the 36 months of our example,
we get
36 * £160.33 = £5771.88. This means we have paid a total of
£771.88 in interest over the three years. As a percentage of the original loan, this
works out at 15.44%, and dividing by three gives a flat rate of 5.15% per annum. This is a useful check and
confirms the rule of thumb that:
A.P.R. equals approximately 2 times flat rate