This means that we should look for a quadratic formula a×n2 + b×n + c

At the moment I am working on my GCSE coursework, and have come up with a problem on sequences.
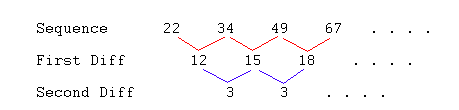
I need a formula for the nth term of a sequence like: |
This is a harder kind of sequence than the ones we explained in response to an earlier query. (Click here to read that earlier message if you have not yet done so.) This kind of sequence is Higher Level work.
The key to finding a formula for the nth term of a sequence is to consider the differences (or "step lengths") between the terms.
If the first differences are constant, then the formula will be a linear function of the form a×n + b where a and b are numbers which you have to work out.
If the first differences are not constant, but the second differences are constant, then the formula will be a quadratic function of the form a×n2 + b×n + c where a, b and c are numbers which you have to work out.
For the sequence you have, we find that the first differences are not constant but the second
differences are constant:

This means that we should look for a quadratic formula a×n2 + b×n + c
We now have to work out the values of the coefficients a, b and c.
For the first term, n=1. Substituting n=1 into the formula gives
a×12 + b×1 + c = 22
This simplifies to
a + b + c = 22For the second term, n=2. Substituting n=2 into the formula gives
a×22 + b×2 + c = 34
This simplifies to
4a + 2b + c = 34For the third term, n=3. Substituting n=3 into the formula gives
a×32 + b×3 + c = 49
This simplifies to
9a + 3b + c = 49
This gives us a set of three simultaneous equations in three unknowns:
| a + b + c = 22 -------(1) |
| 4a + 2b + c = 34 -------(2) |
| 9a + 3b + c = 49 -------(3) |
Solving three simultaneous equations is usually quite tricky, but here the equations are not too bad. Notice that they each have single " + c " at the end. We will first eliminate c to reduce this to two simultaneous equations just in a and b.
Subtract (1) from (2) column-by-column:
3a + b = 12 -------(4)Subtract (1) from (3) column-by-column:
8a + 2b = 27 -------(5)
If you have got this far, you should be happy with solving two simultaneous equations (we hope!).
Check yourself that the two equations (4) and (5) have solutions
a = 1.5 , b = 7.5
Finally replace a and b in the very first equation (1) to find c:
1.5 + 7.5 + c = 22 which means c = 13
So the formula for the nth term of the sequence is:
1.5×n2 + 7.5×n + 13
It would be wise to check this. Replacing n=4 we do indeed find that the fourth term of the
sequence works out to be 67, as it should:
1.5×42 + 7.5×4 + 13 = 24 + 30 + 13 = 67