If an amount A is borrowed and the annual interest rate is P%, then the amount owed after one month is
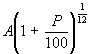

What is meant by the Annualised Percentage Rate (APR), and how is it calculated? |
The APR is intended to give a truer indication of the interest rate being applied (typically to a loan).
Suppose you borrowed £100 for one year, and at the end of the year you repaid £120. The annual interest would therefore be 20% "flat rate".
However, if you repaid £10 per month over the year, you might think that by repaying £120 in total the interest is still 20%. But this is not the case, because you have not had the benefit of the £100 for the whole year.
By paying off the loan in installments, the amount you have borrowed is reducing each month. The £20 interest you are paying is in fact more than 20% of the money owed throughout the year. The APR will take this into account, and it will be a figure higher than 20% when worked out.
A bit of background revision before we go any further...
If an amount A is borrowed and the annual interest rate is P%, then the amount owed after one month is
To calculate the APR in the example above, where £100 is repaid by 12 monthly installments of £10, you need to work out the amount outstanding at the end of each month. By the end of the 12th month, this amount must be zero.
Suppose the APR = P%. Then at the end of month 1 you will have an outstanding
balance of
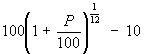
At the end of month 2 you will have an outstanding balance of

A pattern seems to be building up. To see this more clearly, use the following substitution:
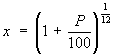
We then have that after 1 month, the amount owed is
100x - 10
After 2 months, the amount owed is
(100x - 10)x - 10
= 100x2 - 10x - 10
Continue this pattern recursively month by month. You will end up with a
very complicated equation with the value at the end of month 12 being equal to
zero:
100x12 - 10x11 - 10x10 - 10x9 - 10x8 - 10x7 - 10x6 - 10x5 - 10x4 - 10x3 - 10x2 - 10x1 - 10 = 0
You will need some computer package (or a numercial/graphical technique) to
solve this.
The actual solution is x = 1.02923 (5 d.p.)
Remember that x was introduced as the substitution for the 12th root of the annual multiplier.
Therefore (1 + P/100) = x12 = 1.0292312 = 1.413 (3 d.p.)
Thus the APR = 41.3%