Integration and Area


  • From: Jon Grundy
  • Date: 27 February 1999
  • Subject: Wrong answer for integration

I had a question to find the area between the x-axis and the curve
y = x^2 - 10x + 16
between x=1 and x=3.

I got the answer 0.666... but the answer is supposed to be bigger.
My teacher says 'sketch the graph' but what has that got to do with it?

Maths Help suggests:

Sketch of y=x^2-10x+16

If you sketch the graph   y = x2 - 10x + 16   you should get something like the picture shown to the right.
We have shaded the required area in green.

The reason your teacher suggested the sketch is that you will notice that the curve
crosses the x-axis between x=1 and x=3.

Check by factorising that the root is at x=2.

When you do the integration, the area above the x-axis will be a positive number,
and the area below the axis will be a negative number.

You should separately evaluate the integrals Integral betweem 1 and 2 and Integral betweem 2 and 3.
Then add the two results, disregarding the negative sign of the second answer.

So: 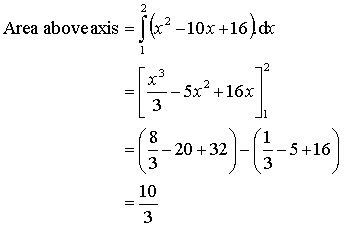Top part, area 10/3 unit^2
and Top part, area -8/3 unit^2

Giving: Total area 6 unit^2

Return to Calculus contents list