Maximum & Minimum Values


  • From: Arron Charman
  • Date: 15 April 1999
  • Subject: Maximum volume of an open tank

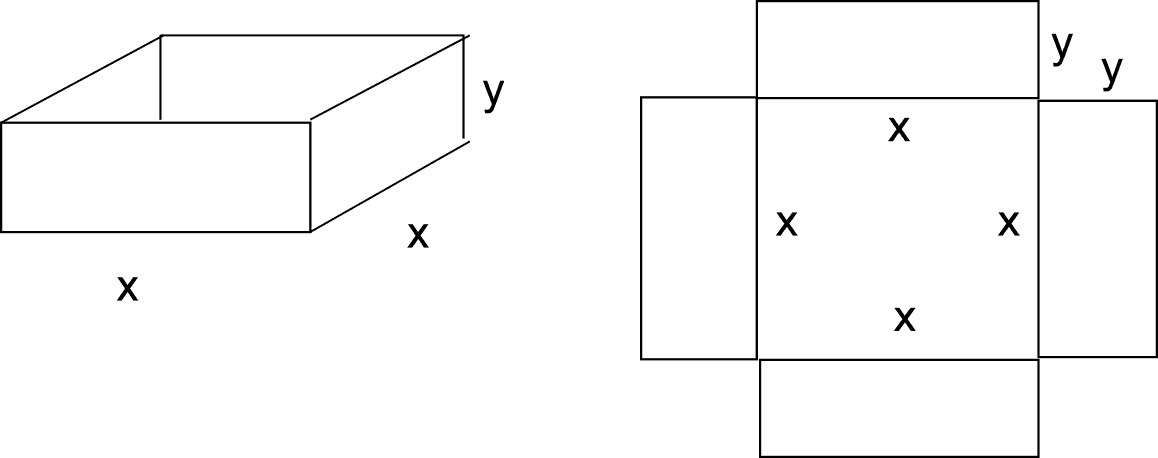
An open rectangular tank has a horizontal square base of side x metres. The height of the tank is y metres. The tanks is made of thin sheet metal. The external surface area of the tank is S square metres and the volume is V cubic metres.
Show that S = 4V/x + x2
Given that V=62.5 find the dimensions of the tank which make the surface area a minimum.

Maths Help suggests:

First of all we need a good diagram of the tank and its net:
Diagram

From the diagram we can work out equations for the surface area and the volume.
The surface area is one square (x by x) and four rectangles (y by x)
So S = x2 + 4xy . . . . . (1)

The volume is given by base area (x2) times height (y)
So V = x2y . . . . . (2)

The equation we are asked to prove contains S, V and x but not y, so use equations (1) and (2) above to eliminate y as follows:
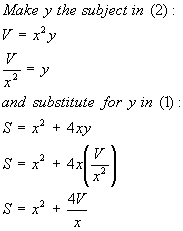
S=4V/x + x^2
which is the equation required.

Now replace V by the given value 62.5 and differentiate with respect to x:
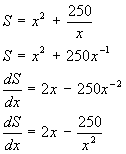
dS/dx = 2x - 250/x^2

The maximum or minimum value of S is given when dS/dx = 0
x=5

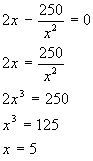
So the base is a square of side 5 metres. The height y can be found by replacing x by 5 in the equation used for eliminating y above:
y=2.5

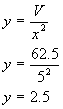
Finally we need to check whether the surface area is a maximum or a minimum when x=5 and y=2.5
This can be done by considering the gradient either side of the point when x=5
We draw up a table:
x456
dS/dx-7.62505.056
From this we see the gradient goes from negative through zero to positive, meaning the point is a relative minimum.

Therefore the tank which meets the stated requirements with a minimum surface area has base 5 metres by 5 metres and height 2.5 metres.

We may wish to check this answer. Plot the graph of the surface area S = 250/x + x2
Graph
The minimum point does indeed seem to be where x=5, and this can be confirmed by zooming in.

Return to contents list