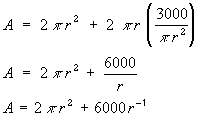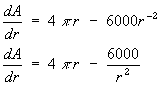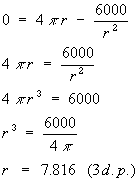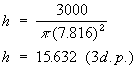Optimisation
- From: Natasha Squires
- Date: 14 Feb 1999
- Subject: Minimum surface area of a tin can
What are the dimensions of a closed cylindrical tin can which holds a
volume of three litres using the minimum surface area of material
(ignoring any overlaps)?
|
Maths Help suggests:
This is a very common type of problem in calculus courses.
The first thing to do is to draw diagrams of the can and its net.
The unknown dimensions are the base radius r, and the height h.
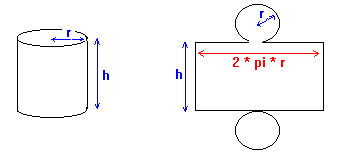
Note that the curved side of the can opens out to a rectangle whose length
is the same as the circumference of the circular top (2*pi*r).
Apologies for typing "pi" instead of the Greek symbol!
Start by writing down what we know, namely that the volume is 3 litres
which is the same as 3000 cubic centimetres (let's decide to use cm as
our basic unit of measurement):
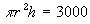 - - - - Equation (1)
- - - - Equation (1)
Now write down what we are interested in. We want to find the minimum
surface area of the can. The surface area is made up of two circles plus
one rectangle. The formula is:
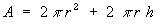
The standard technique to find the minimum (or maximum) value of a function
is equate the first derivative to zero. However, it is not possible
to differentiate the Area function shown above, because it contains
two variables, r and h. We must first eliminate one of the
variables. Look back at the Volume equation (1). Make h the subject:
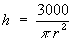 - - - - Equation (2)
- - - - Equation (2)
and substitute for h in the Area equation, giving:
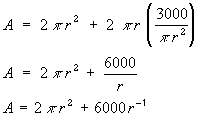
The area A is now given as a function of one variable only (r).
We can now differentiate it with respect to r, giving:
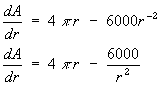
The minimum surface area will be given when dA/dr=0. Solve this for r:
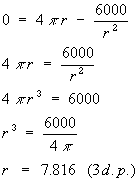
Now that we know what r is, we can substitute it back into Equation (2)
to find the corresponding value of h:
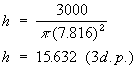
So the dimensions of the can which will hold 3 litres using the minimum
surface area of material are:
- Base radius = 7.816 cm
- Height = 15.632 cm
It is worth checking these values in the original volume equation
to show that pi * 7.8162 * 15.632 = 3000
NOTE 1
We have not actually proved that the surface area is a minimum when
the can has these dimensions. There are two ways of doing this:
(i) Go back to the equation for dA/dr. Remember that dA/dr tells you
the gradient. If dA/dr is negative for a value of r slightly to the left
of the optimum value (say r=7.5), and dA/dr is positive for a value of r
slightly to the right of the optimum value (say r=8.0), then the area
function decreases, reaches a minimum, and increases. (Check this!)
(ii) If the second derivative is positive at the optimum point,
then the point is a minimum. (Check this, by finding d2A/dx2
and evaluating it at r=7.816)
NOTE 2
It is an interesting result that the optimum dimensions of a closed
cylinder are always when the height is twice the base radius, or
height = base diameter. How many tin cans in real life actually have
this optimal shape?
Return to Calculus contents list


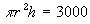 - - - - Equation (1)
- - - - Equation (1) 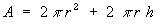
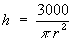 - - - - Equation (2)
- - - - Equation (2)