Optimisation


  • From: J W
  • Date: 12 March 1999
  • Subject: Maximum area of isosceles triangle

How can you prove that for an isosceles triangle with a set perimeter,
the triangle with the largest area is always equilateral.

I think you must differentiate, but how?

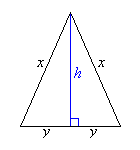
Diagram of isosceles triangle of sides x,x,2y

Maths Help suggests:

Start by drawing a diagram (right) of an isosceles triangle with two equal sides x and base 2y.

Let the perimeter be P. Then the length y is:

y = 1/2 (P-2x)

..and the height h:

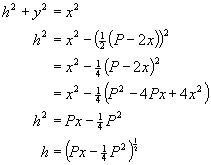
Use Pythagoras to get height

Develop an expression for the area A in terms of x:

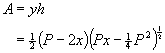
Area = 1/2 x base x height

To find the maximum area, differentiate A with respect to x
using the product rule:

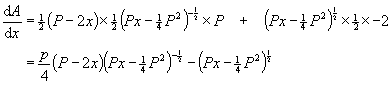
Differentiate using Product Rule

...and set the derivative to zero (for max or min value of A):

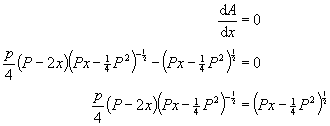
Set derivative to zero

Solving for x:

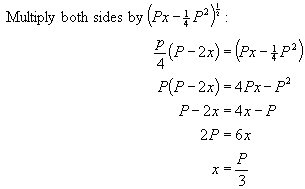
Solving for x gives x=P/3

So the sides are each one third of the perimeter, and the triangle is equilateral.

(We leave it as an exercise to verify that x=P/3 does result in a maximum area.)

Return to Calculus contents list