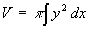
Using the function and the values in your question, you need to find
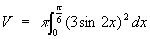

Find the volume generated when the part of the curve y = 3sin2x between the limits x=0 and x=pi/6 is rotated around the x-axis. Please help me with this problem - every time I try it I get a different answer! |
This is a question about Volumes of Revolution. You need to use the formula
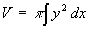
Using the function and the values in your question, you need to find
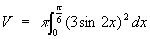
First of all, this simplifies to
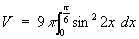
Where most people get stuck is that they do not know how to integrate a squared trig function. At A-level, there is a standard procedure for this:
To integrate sin2x or cos2x use the double angle identities:
cos2A = 2cos2A - 1 from which cos2A = (1 + cos2A)/2
cos2A = 1 - 2sin2A form which sin2A = (1 - cos2A)/2
In your case the basic angle (A) is 2x so the double angle (2A) will be 4x.
You equation becomes:
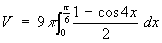
and the solution proceeds as follows (remember to use the standard surd form for sin(2pi/3), or
make sure your calculator is in radian mode)

The answer given above is in "exact form", which is expected at A-level.
The decimal equivalent
is V = 1.382 cubic units (3 d.p.)