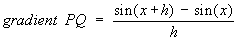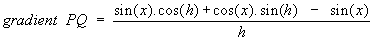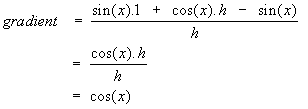Differentiation
- From: J Sanders
- Date: 17 Feb 1999
- Subject: Differentiating sin(x)
I am on an engineering course. We are doing differentiation in our
maths classes. The lecturer just told us that if you differentiate
sin(x) you get cos(x). He said don't worry about why, just accept it.
But it seems a strange result to me. Can you tell me if it really is
true, and why it works?
|
Maths Help suggests:
First of all, it really is true that the derivative of sin(x) is cos(x).
We don't agree that this result is "strange" - it is actually very neat!
A formal proof needs quite a lot of background maths - perhaps that is
why your lecturer told you not to worry about it for now. But it is
quite a useful piece of theory, so we will outline it here . . .
First, remember that for any function, the derivative dy/dx represents the
gradient at a particular point P with coordinates P(x,y).
Look at the diagram below:
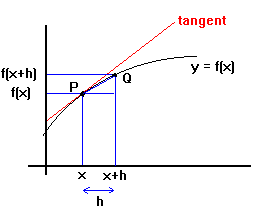
The gradient of the curve y = f(x) at point P is the same as the gradient
of the tangent to the curve at point P (shown in red).
This is approximately the same as the gradient of the line joining
P and a nearby point Q (shown in blue).
h stands for the small distance along the x axis that Q is away from P.
Do you agree that the closer Q gets to P, the closer the line PQ gets to
the red tangent at P?
Therefore, we can say that the gradient at P (red) is essentially the same as
the gradient of PQ (blue) as the distance h tends to zero.
Now the curve you are interested in is y = sin(x).
So P has coordinates (x , sin(x)) and Q has coordinates (x+h , sin(x+h)).
The gradient of PQ (look at the blue triangle) is "y-step over x-step"
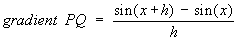
We now need to simplify this, using an important result in trigonometry:
- sin(A + B) = sin(A).cos(B) + cos(A).sin(B)
Using this in the equation above, with A=x and B=h, gives:
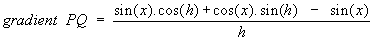
So as h tends to zero, this gives us the gradient of the curve y=sin(x)
It is now time to use two more important trig results:
- If h tends to 0 (which we are assuming, because Q gets close to P)
Using these facts, we obtain
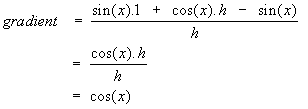
Therefore the gradient of the tangent at P is given by cos(x),
which is the same as saying that the derivative of sin(x) is cos(x).
Return to Calculus contents list