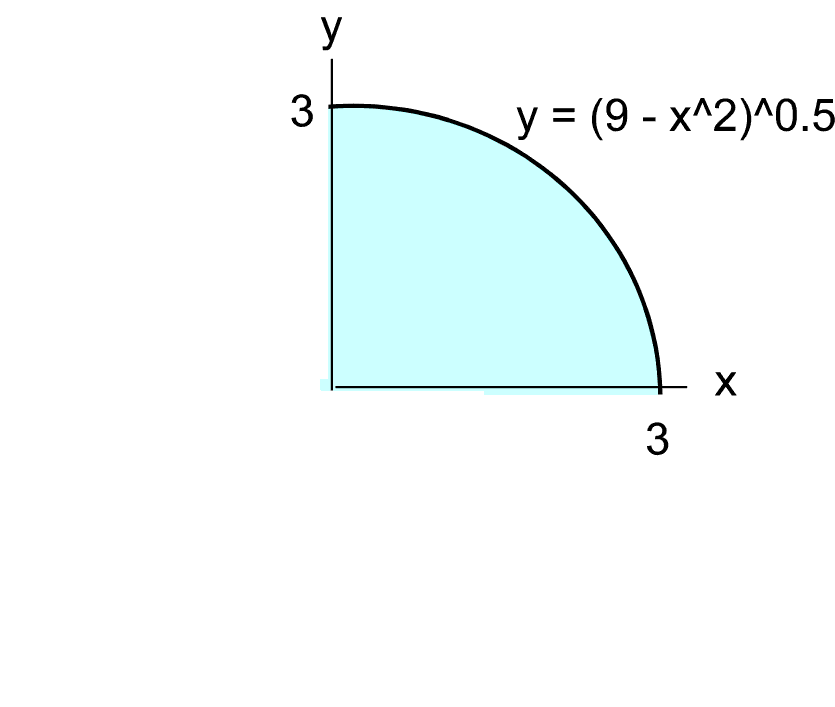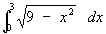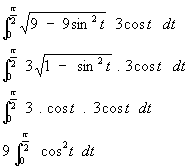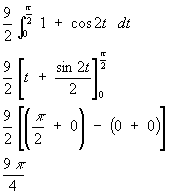Use integration to find the area of the region bounded by the curve Please help - the question doesn't say what limits of integration to use, so how can you do it? |
The question expects you to recognise the equation. It is the equation of a circle centred at the origin (0,0) with radius 3 units.
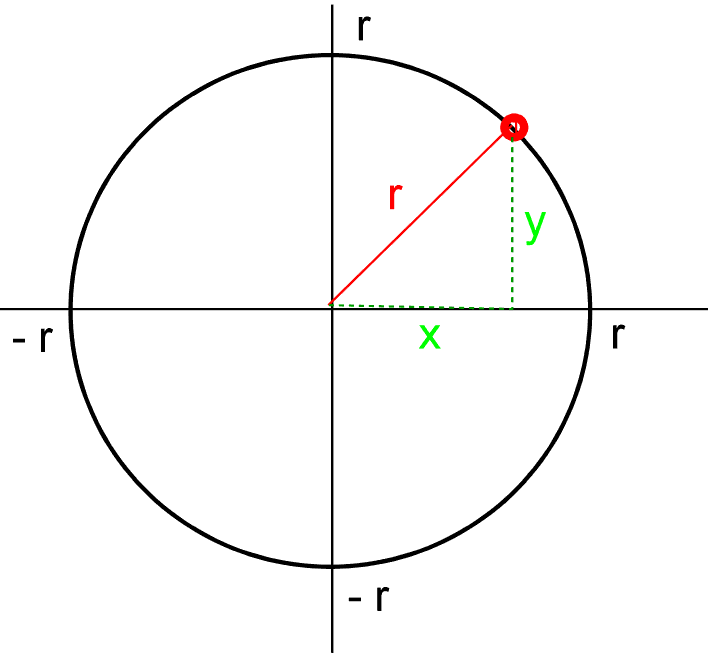The general equation of a circle centred at the origin with radius r is
x2 + y2 = r2
For a visual proof of this, look at the diagram. Choose any point on the circle, and construct
a right-angled triangle. Pythagoras' Theorem tells us that the x-coordinate squared plus the y-coordinate
squared equals the radius squared. Hence the equation above.
In your equation the value of r2 is 9, so the radius of your circle is 3.
The simplest way to find the area by integration is to consider one quadrant (quarter-circle)
and multiply the answer by 4. (See diagram below). Also we need to make y the subject of the
equation:
y = sqrt(9 - x2)
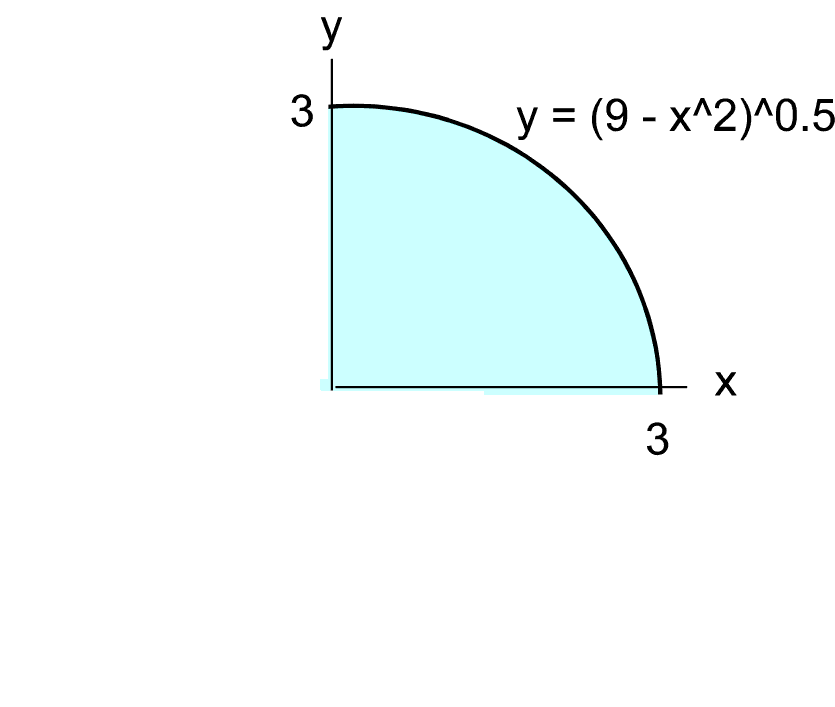
The area of the blue quadrant is therefore given by the integral
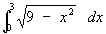
To evaluate this integral, you need to make a substitution:
Let x = 3 sin(t)The integral then simplifies as follows:
then dx = 3 cos(t) dt
x = 0 implies 3 sin(t) = 0 implies t = 0
x = 3 implies 3 sin(t) = 3 implies t = pi/2
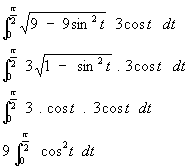
Remember now how to integrate cos2x
Use the identity
cos(2A) = 2 cos2A - 1 which rearranges to
cos2A = (1 + cos(2A))/2
Using this identity we can finish the integral as follows:
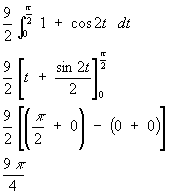
Don't forget, this is the area of a quarter circle. Therefore the full circle has area 9*pi
We can check using the well-known formula A = pi*r2 that this answer is correct.
Using integration to find the area of a circle is like using a sledgehammer to crack a nut. However, this question does show us that the techniques of integration are valid in finding the area of curve-bounded shapes.