Quadratic functions

Maths Help suggests:

We agree with you that factorising quadratics can take a lot of
time-consuming trial and error, especially if the coefficients are large.
However, it is worthwhile giving it a try, since with practice you will
be able to identify possible factors more quickly.

Yes, there is a way to tell in advance whether a quadratic will factorise
neatly. You need to calculate the discriminant of the quadratic.
Assuming you have the quadratic in the standard format

• ax² + bx + c = 0

If the discriminant is a perfect square (such as 4, 25, 49, 100 etc),
then the quadratic will factorise neatly.

For example, 2x² - 13x - 24 has discriminant
(-13)² - 4(2)(-24) = 361 = 19² , a perfect square.
This means the quadratic will factorise, and the factors turn out to be
(2x + 3)(x - 8)

It is quite easy to understand why this works. The discriminant b² - 4ac
appears under the square root sign in the well-known formula for
solving quadratics: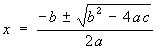
If the discriminant is a perfect square, the square root in the formula
will give a "nice" whole number, meaning the solutions will be rational
(i.e. whole numbers or fractions), meaning factors with "nice" coefficients
exist. Conversely, if the discriminant is not a perfect square, the square
root will be irrational (nasty non-recurring decimal), meaning the solutions
are irrational, something which will not occur if the quadratic
factorises neatly.

Of course, if the discriminant is negative the quadratic has no
real solutions at all (because the square root of a negative number is
not defined among real numbers), so the quadratic will then definitely
not factorise.

Here is a little test to finish with:
Only one of the quadratics below factorises neatly. Which one?

• 12x² + 57x + 72
  
• 12x² + 59x + 72
  
• 12x² + 61x + 72