
The table below gives experimental values of a quantity S for various times t:
t-squared, and estimate the constant of proportionality. |
If S is proportional to t2 then we would have the relationship
S = k.t2
This means that a graph of S plotted against t2 will be:
So first we need to draw up a new table of S and t2:
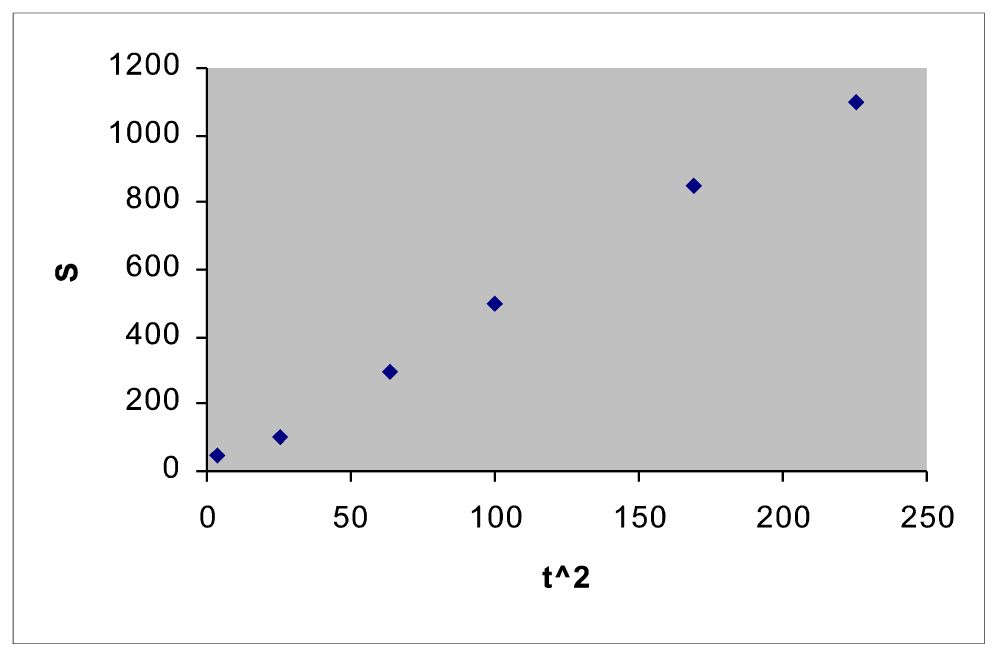
| t2 | 4 | 25 | 64 | 100 | 169 | 225 |
| S | 50 | 100 | 300 | 500 | 850 | 1100 |
Plotting this will give the following graph:

The fact that the data points lie very close to a straight line through the origin verifies that
S is proportional to t2
To find the value of the constant of proportionality, mark in the line of best fit on
your graph (remember to make it pass through the origin). It should look like this:

Use your line of best fit to mark in a gradient triangle. This should connect any two
easy-to-read points which lie on your line of best fit (not necessarily any of the actual
data points).
On our graph, the points are at approximately (80,400) and (160,800)
Therefore y-step = 400 and x-step = 80
and the gradient = y-step/x-step = 400/80 = 5
Note that if you plotted the graph yourself on graph paper, you would be able to read off
the points and find the gradient much more accurately.
Therefore we can conclude that the data is related by the approximate rule
S = 5 t2
NOTE: It is possible to use some graphical or programmable calculators, or spreadsheets, to find a best fit rule of the form y = a x2 and to establish the correlation. Refer to your calculator handbook or ask your teacher for details.