
The function f is given by f:x --> ln(4 - 2x), x<2
When it comes to e and ln, I become all quivery at the knees!!! |
Just as addition and subtraction are inverse processes (each 'undoes' the other),
and squaring and square rooting are inverse proceses,
ex and ln x are inverse processes.
To solve your problem, let y = f(x) then make x the subject:
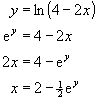
This function of y is the form of the inverse of the original function of x.
Write the inverse function as ![]()
The range of the inverse function f-1(x) is the domain of f(x), namely x < 2.
To make a successful sketch of the inverse function, you should work out
the y-intercept and get the general shape right:
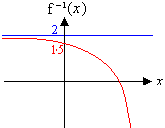
Convince yourself that this can be built up from the basic graph of y = ex
as follows:
REMEMBER that a useful way to get the graph of an inverse function is to reflect the
graph of the original function in the line y=x. We have not done that here for two reasons.
Firstly, the graph of f(x) is itself not so straightforward to sketch (it needs a series of
transformations of the basic graph y = ln(x)). And secondly, in this particular question, the graph
of f(x) and its inverse overlap quite considerably. We suggest you investigate them using a
graphics calculator or computer graph plotter.