3y = 2x
y =

I have this question and I am unsure what it means and how to go about answering it: Sketch the regions in the positive quadrant of the (x,y)-plane defined by the inequality constraints:
|
The first inequality, 2x < 3y is equivalent to asking:
"What numbers x and y will mean that
2 times x is less than 3 times y ?"
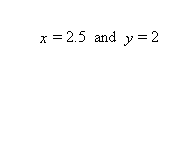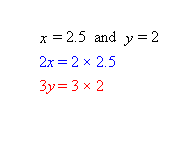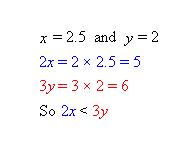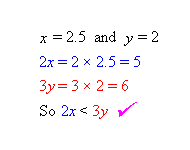
There are infinitely many solutions to this question, for example x = 2.5, y = 2
Because all of these solutions come as pairs of numbers for x and y, we can write them as coordinate pairs.
The question is asking you to colour in a region on a graph
where all the pairs of x, y coordinates satisfy the inequality.
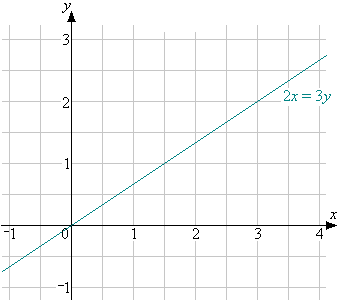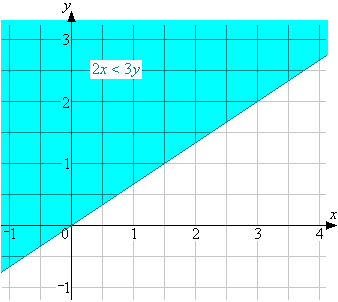
The boundary of the region 2x < 3y is a straight line.
The equation of this straight line is 2x = 3y.
To plot this straight line, make y the subject:
3y = 2x
y = ![]() x
x
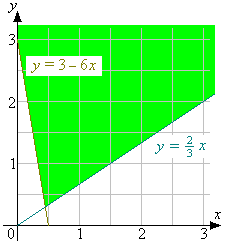
The region 2x < 3y is everything to the left of the line 2x = 3y
(To the left because 2x is less than 3y.)
Note that in your case you only need to sketch the graph in the positive quadrant,
which means only for positive values of x and y.
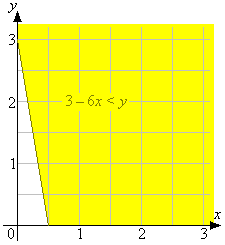
The answer to the second part is the region above the line y = 3 - 6x:
The answer to the third part is the region where both of the inequalities are satisfied: