Complex Numbers


  • From: Lee Armstrong
  • Date: 3 March 1999
  • Subject: Solve this quadratic with complex coefficients

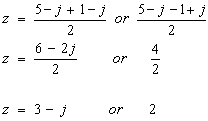
Can you show me how to solve the equation
z2 + (-5 + j)z + 6 - 2j = 0

None of us could do it in class - even the teacher got stuck!

(I am doing Further Maths A-level)

Maths Help suggests:

Preliminary comment: This topic of complex numbers occurs in the "further" pure maths syllabus at A-level. Complex numbers are also dealt with in some higher engineering courses.
Some textbooks use i for the imaginary value sqrt(-1), some use j.
In this question, j2 = -1

Let's look closely at your equation.

z2 + (-5 + j)z + 6 - 2j = 0
This is basically a quadratic, in the usual form
az2 + bz + c = 0
where a,b,c are coefficients. The only special thing here is that they are complex:
a = 1
b = -5 + j
c = 6 - 2j
Substituting these values into the well-known equation for the roots of a quadratic, we get
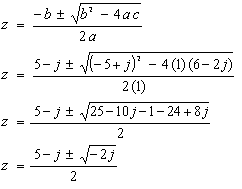
(5-j+/-sqrt(-2j))/2

At this stage we pause - what is the square root of -2j? Finding the square root of a complex number is fairly tricky (but it is an important technique in Further Pure Maths A-level papers). We will explain at the end of this page how to do it.

For now, just accept that:
sqrt(-2j) = 1 - j OR -1 + j
Using this "fact", we proceed to the solution:
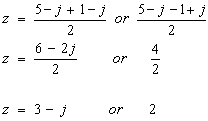
z = 3-j OR 2

How do we check these solutions are correct? The long way is to substitute them for z in the original equation, and verify that the left hand side does simplify to 0. A neater way is to recall the standard result for roots of quadratics:

Sum of roots = -b/a
Product of roots = c/a
I suggest you carry out each of these checks for practice.

Finding the square root of a complex number

EXAMPLE
Find the square root of 7 + 24j

METHOD
We assume that the answer will be another complex number. Call it u + vj, where u and v are real numbers. Thus:

u + vj = sqrt(7 + 24j)
(u + vj)2 = 7 + 24j
u2 + 2uvj + v2j2 = 7 + 24j
u2 + 2uvj - v2 = 7 + 24j
Comparing real and imaginary parts gives us two simultaneous equations in u and v:
u2 - v2 = 7 ....(1)
2uv = 24 ....(2)
From (2) we have
v = 12/u
Substituting for u in (1) gives:
u2 - 144/u2 = 7
u4 - 144 = 7u2
u4 - 7u2 - 144 = 0
(u2 - 16)(u2 + 9) = 0
u2 = 16 OR u2 = -9
The second option is not possible, because u must be real (see statement at the beginning).
u2 = 16
u = 4 OR -4
Substituting these values for u back in (2) gives
when u = 4 , v = 3
when u = -4 , v = -3
Therefore the square roots of 7 + 24j are
4 + 3j OR -4 - 3j
NOTE: Just as with real numbers, there are two square roots of a complex number, of opposite signs.

EXERCISE:
Use the method above to show that sqrt(-2j) = 1 - j OR -1 + j

Return to contents list