It is a way of re-writing a quadratic function in order to see some of its key features.
The "completed square" form of a quadratic function is in general:

How do you complete the square? |
Completing the square is a standard technique at A-level.
It is a way of re-writing a quadratic function in order to see some of its key features.
The "completed square" form of a quadratic function is in general:
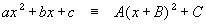
To understand the procedure, you must first understand what happens
when you square a bracket containing x plus/minus a number.
Convince yourself that the examples below are true:
Note that the coefficient of x on the right hand side is
double the number in the squared bracket on the left.
Here is another example which shows this:
So if you start with a quadratic in the form x2 + px + q
then you know the number in the bracket must be half of p.
For example,
Now go back and look again at the group of four examples above.
When you square out the bracket on the left, you always end up with
the number squared on the right. For example:
Now let's put all this together . . .
EXAMPLE: Complete the square on x2 + 16x + 3
Start with x2 + 16x
The bracket would contain x + 8 , because 8 is half of 16.
Now (x + 8)2 = x2 + 16x + 64
Subtract 64 from both sides to obtain
x2 + 16x = (x + 8)2 - 64
The left hand side plus 3 is equal to the original function in the question
so add 3 to both sides:
x2 + 16x + 3 = (x + 8)2 - 64 + 3
and tidying up the constants on the right hand side gives
x2 + 16x + 3 = (x + 8)2 - 61
The expression on the right is the "completed square" form.
ANOTHER EXAMPLE (with fewer words)
Complete the square on x2 - 3x - 8
Half of the x-coefficient is -1.5 , so start with
(x - 1.5)2 = x2 - 3x + 2.25
Then
(x - 1.5)2 - 2.25 = x2 - 3x
and
(x - 1.5)2 - 2.25 - 8 = x2 - 3x - 8
So the answer is
(x - 1.5)2 - 10.25
A MORE COMPLICATED EXAMPLE
Express 2x2 + 5x - 1 in the form A(x + B)2 + C
The first step is to take out a factor of 2, in order to start with a single x2
2 [ x2 + 2.5x - 0.5 ]
Complete the square as usual inside the square brackets:
2 [ (x + 1.25)2 - 1.5625 - 0.5 ]
2 [ (x + 1.25)2 - 2.0625 ]
Finally multiply the square brackets out by 2, giving
2(x + 1.25)2 - 4.125
THE MAIN REASON FOR COMPLETING THE SQUARE
The "completed square" form of a quadratic function shows you immediately
the coordinates of the maximum or minimum point of the function.
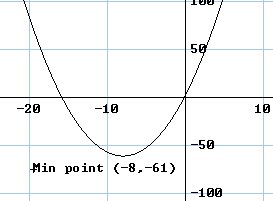
Suppose you had the graph of the function of the first example above, namely
y = x2 + 16x + 3
Completing the square gives the equivalent form
y = (x + 8)2 - 61
Now the minimum value of a squared quantity is zero.
Therefore the minimum value of (x + 8)2 - 61 is 0 - 61 = -61
The squared bracket will take its minimum value of zero when the expression inside it is zero,
namely when x + 8 = 0 , or x = -8
Therefore the minimum point of the graph is at y = -61 , when x = -8.
This can be confirmed by plotting the graph: