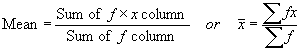

Please help me understand how to find the standard deviation of grouped data. |
We suggest you set out your calculation using a table with headings:
| Class | Midpoint (x) | Frequency (f) | f × x | f × x2 |
Notice these are all the headings you need to work out the mean,
plus an extra "fx2" column.
Work out the mean using:
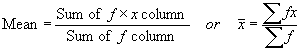
(Click here to see an example of working out the mean of a grouped distribution)
... and the variance using this formula:
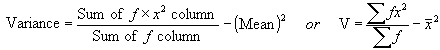
Square root the variance to calculate the standard deviation.
Here is a worked example:
|
100 parcels were weighed. Their masses were as follows:
Estimate the mean and standard deviation of the masses. |
Draw a table like this:
| Mass, g | Midpoint (x) | Frequency (f) | f × x | f × x2 |
| 0-250 | 125 | 7 | 875 | 765625 |
| 250-500 | 375 | 18 | 6750 | 2531250 |
| 500-750 | 625 | 33 | 20625 | 12890625 |
| 750-1000 | 875 | 26 | 22750 | 19906250 |
| 1000-1500 | 1250 | 16 | 20000 | 25000000 |
| Totals: | 100 | 71000 | 61093750 | |
The estimate of the mean is:
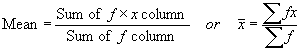
mean = 71000 ÷ 100 = 710 grams.
The estimate of the variance is:
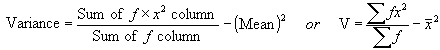
var = 61093750 ÷ 100 - (710)2 = 106837.5
...and the standard deviation is the square root of the variance:
standard deviation = sqrt(106837.5) = 326.86 grams (2dp)