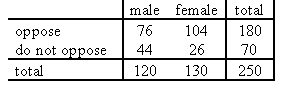
This is an example of a 2-by-2 contingency table (2 rows, 2 columns).

I have got to do a chi-squared test for my A-level biology project. |
First, let us remind ourselves what the chi-squared test is used for.
If you cross-reference two descriptive attributes of your sample, the frequencies (i.e. number of people/items) in each sub-category can be drawn up in a contingency table
For example, if you interview 250 adults (120 male, 130 female) and find
that 76 of the 120 men oppose vivisection whereas 104 of the 130 women
oppose vivisection, you could draw up a table as shown:
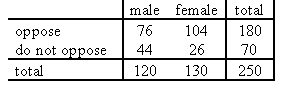
This is an example of a 2-by-2 contingency table (2 rows, 2 columns).
The chi-squared test will enable you to determine whether there is evidence that one gender is significantly more likely to oppose vivisection that the other (i.e.whether there is a significant association between the attributes). This is done by calculating the expected frequencies for each cell (NB a 2-by-2 table has four cells) and comparing the expected frequencies with the observed frequencies of your survey. (We assume you are happy about the procedure for doing this.)
Now to answer your question about sample size . . . .
It is a standard assumption that the expected frequency of each cell must be at least five for the chi-squared test to be valid. This means that if the expected frequency of the least likely cell is at least five, then the expected frequencies of most cells will be considerably bigger than five.
As a rough rule, if you anticipate the sample to fall roughly equally between the subcategories (for example if you plan to survey half men and half women, and you have reason to believe that the other attribute is divided roughly equally between your classes), you should aim for a minimum sample size of approximately (Number of Cells) × 10.
However, if you anticipate that some of your subcategories may be more common
than others, you should scale up accordingly. For example, if you are comparing
"satisfaction level" (good/average/poor) against "age" (under-65/over-65)
and you have reason to believe average to be twice as likely as good or poor, and three
times as many under-65s as over-65s, then a rough plan might be:
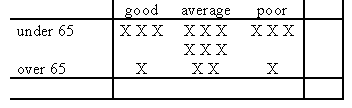
and taking X as 10-ish as before would suggest a sample size of at around 160.
Note that the larger the dimensions of your contingency table, the larger your sample size will need to be to ensure an expected frequency of 5 in each cell. So think twice before setting up an experimental design with unnecessarily many options or subcategories.