the relationship
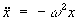
is true for some value of w (sorry, can't type the Greek "omega" here!)
Remember that "x-double-dot" stands for acceleration.

The position of a particle from point O at time t is given by
I answered this question by saying that cos is an oscillating function |
To formally demonstrate simple harmonic motion, you must show that
the relationship
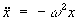
is true for some value of w (sorry, can't type the Greek "omega" here!)
Remember that "x-double-dot" stands for acceleration.
We are given the displacement x at time t.
Differentiating this with respect to t gives the velocity, and
differentiating again gives the acceleration. Thus we obtain
Looking at the expressions above for displacement and acceleration,
we see that acceleration = - 4 times displacement
This is the required format for SHM (see box above), with w = 2.
I think this is what your teacher is looking for.