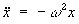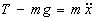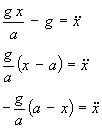In A-level Mechanics we have the following question: A particle of mass m is attached to one end of a light elastic string of natural length a and modulus mg. The other end of the string is fixed to a point A.Please help - this question has really thrown me! |
The general method for this type of question (proving SHM for particles dangling on the end of
an elastic string) requires you to show that the acceleration is a negative multiple of the distance
of the particle from the centre of oscillation, namely:
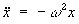
This is normally done by applying Newton's 2nd Law ("F=ma") when the particle is a general
distance x from the centre of oscillation. This question is slightly different in that
x is measured from the point O, but that will sort itself out as we work through the
question. Also, the tension in the string will be given by Hooke's Law.
Firstly, a good diagram is essential: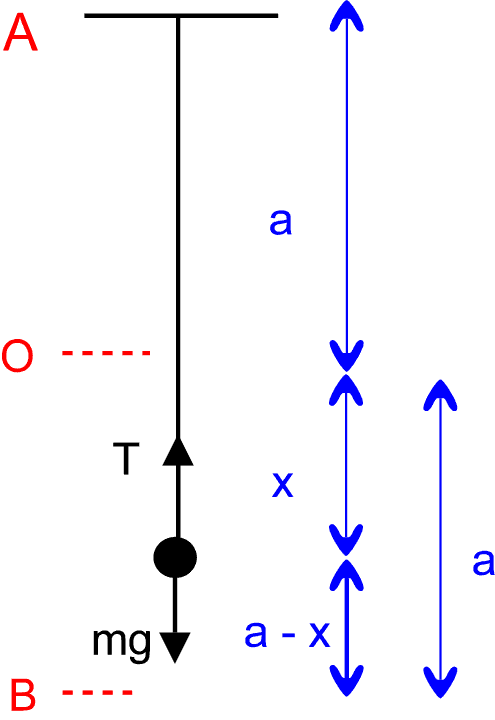 
Apply Newton's 2nd Law ("F=ma") with the upward direction positive:
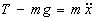
Use Hooke's Law for the tension in the string:
Simplify:
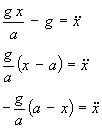
Thus we see that the acceleration is a negative multiple of the distance of the particle from the centre of oscillation (here a-x rather than x). This proves that the particle performs S.H.M. for as long as the string remains taut (ie when T exists as shown).