Conical Pendulum


  • From: Martin Gee
  • Date: 16 Feb 1999
  • Subject: Have I got enough information?

I was given this question:

A conical pendulum is made by fixing one end of a light inextensible string to a small bob B and the other to a fixed point P. The bob is rotating in a horizontal circle with angular velocity 2 rad·s-1.
Find the vertical distance of B below P.

I do not know the length of the string, the mass of the bob, the angle the string makes with the vertical, or anything!
I don't think the question is possible to answer. Am I right?

Maths Help suggests:

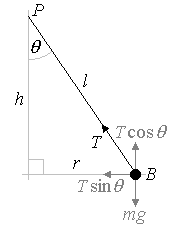
Diagram of System

Surprisingly, it is possible to solve this problem!
Let's start by sketching a vertical section of the pendulum.

Notice that we have given symbols to all the unknown features of the problem, each of which (except h of course!) we will try to eliminate.

Resolving vertically and horizontally:
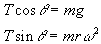
Tcos(theta)=mg, Tsin(theta)=mrw^2

Let us first eliminate the unknown angle from the above...
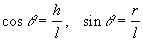
cos(theta)=h/l, sin(theta)=r/l

... leaving us with:
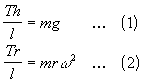
(Th)/l=mg, (Tr)/l=mrw^2

Solving (2) for T gives
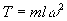
T=mlw^2

And substituting into (1):
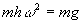
mhw^2=mg

Which yields:
h=g/(w^2)

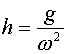
So, in this case, the correct distance is g/4

Back to contents list