Complex Numbers

Maths Help suggests:

Complex numbers have two parts:

• A real part, and
• an imaginary part.

The imaginary part is a multiple of the number j:

Examples

The numbers   4 + j3,   -1 + j5,   -j3   are all examples of complex numbers.

Note that mathematicians sometimes use the symbol i for the square root of -1.
Engineers use i for other quantities (e.g. electric current) and j for complex numbers.

Separately add the real parts and the imaginary parts.

Example

(4 - j3) + (-1 + j5) = 3 + j2.     Because (real parts) 4 + (-1) = 3   and   (imaginary parts) -j3 + j5 = j2.

Separately subtract the real parts and the imaginary parts.

Example

(2 + j7) - (-1 + j3) = 3 + j4.

Multiply out the brackets term by term. Replace j² with -1.

Example

Multiply top and bottom of the division by the Conjugate of the bottom.
(The Conjugate of a complex number is what you get when you change the sign of the imaginary part.)

Example

The conjugate of   1 + j2   is   1 - j2.

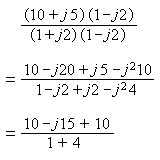
The bottom part always simplifies to a real number (in this case 5). So:

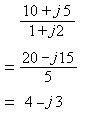
You can check that (4 - 3j)(1 + 2j) = 10 + 5j